Hoofdstuk 3: Kansrekening: Willekeurigheid
 Gebeurtenissen
Gebeurtenissen
Over het algemeen is het doel van een kansexperiment niet om simpelweg het resultaat waar te nemen, maar juist om te bepalen of het resultaat aan een bepaald criterium voldoet. Zo zouden we bijvoorbeeld bij het gooien van een dobbelsteen geïntereseerd kunnen zijn in of er een even getal gegooid wordt.
Met andere woorden, wat we graag willen weten is of de geobserveerde uitkomst deel uitmaakt van een specifieke deelverzameling van de uitkomstenruimte. Een dergelijke deelverzameling wordt een gebeurtenis genoemd.
Gebeurtenis
Een gebeurtenis is een deelverzameling van de uitkomstenruimte.
Stel je een kansexperiment voor waarbij we twee keer een muntje opgooien. Gebeurtenis #A# wordt gedefinieerd als:
A = 'er wordt minstens één keer Kop gegooid'
Geef alle uitkomsten van dit experiment die onderdeel uitmaken van gebeurtenis #A#.
#A = \text{'er wordt minstens één keer Kop gegooid'} = \{KK,KM,MK\}#
De uitkomstenruimte van dit experiment is: \[\Omega = \{KK, KM, MK, MM\}\]
Van deze uitkomsten voldoen er drie aan het criterium gesteld door gebeurtenis #A#:
\[A=\{KK,KM,MK\}\]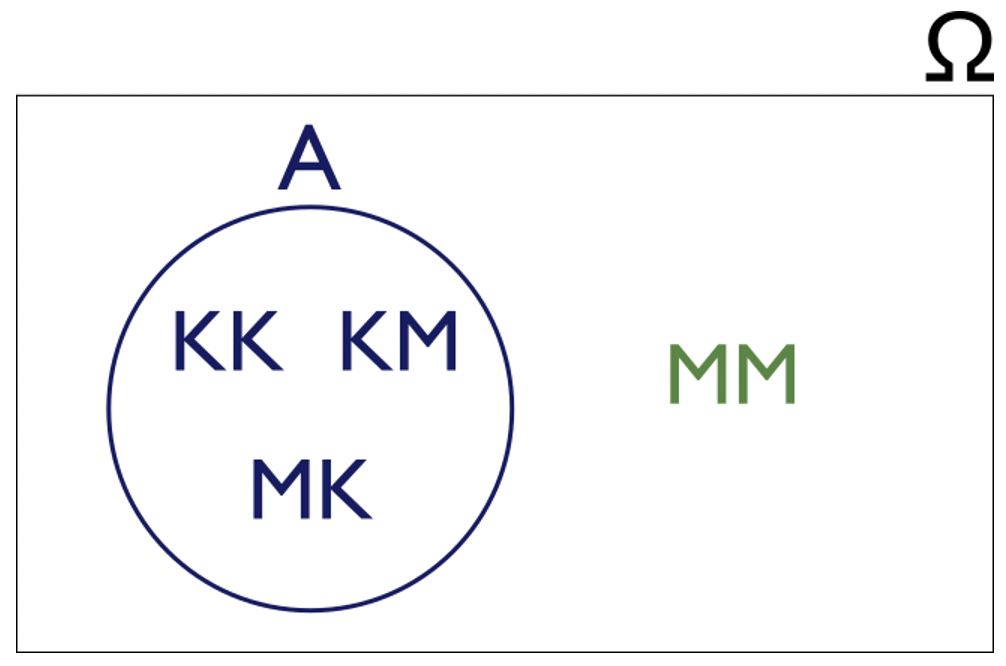

omptest.org als je een OMPT examen moet maken.



